
|
User Guide |
| User Guide | Transform Guide | OSW on the Web | |
6. Advanced Sound-Synthesis in OSW
In the previous chapter, we explored a variety of techniques for manipulating sound signals in OSW, mostly using waveform representations. Waveform representations of sound are similar to image representations of visual scenes. Images allow efficient transformations on groups of pixels, but very little control over perceptual or geometric features. When such control is required, a vector- or program-based representation (e.g, PostScript) is preferred. These representations are also a form of compression in that they require less space than the images they represent. Sounds can also be represented by programs, with similar advantages for compression and mutability [Scheirer 2000]. The process of generating sound from programs is called sound synthesis. This chapter describes the more advanced synthesis techniques available in OSW, building on the concepts of oscillators and filters presented in the previous chapter. Some of the material in the chapter is based on earlier work [Chaudhary 2001] adapted for OSW.
Consider a synthesis function of a pure tone with constant pitch, such as that generated by the Sinewave transform:
where A and f represent the peak amplitude and frequency of the sinusoid, respectively. Instead of storing the entire duration (e.g., several seconds) of the waveform as an audio file, one need only store the instructions to generate the the waveform and the parameters A and f. This information can be stored in a compact representation such as an OSW patch and used to generate an arbitrarily long waveform as needed. Additionally, controlling the pitch in the patch-based functional representation is accomplished by simply scaling the parameter f, whereas changing the pitch of a stored waveform representation requires complex sample-rate conversion operations to avoid loss of quality (e.g. anti-aliasing to avoid degrading a scaled image).
Controlling synthesis parameters: Envelopes and Modulators
The parameters of a synthesis function such as a Sinewave can of course be time varying. Thus, we can represent tones of varying pitch and amplitude functionally:
The varying amplitude and frequency parameters A(n) and f(n) can represent variations in user input over time, as in the following patch:

These parameters can also be described by functions in OSW. Functions that control synthesis parameters are called envelope functions. An example of an envelope function that controls the amplitude of an oscillator can be found in the amplitude envelope tutorial patch. While envelope functions are often breakpoint functions (i.e., like the control points of curves in graphics), the can themselves be oscillators. In amplitude-modulation (AM) synthesis, the amplitude parameter A(n) is representated by an oscillator, as illustrated in the AM tutorial patch. In frequency-modulation (FM) synthesis, the frequency parameter f(n) is an oscillator, as illustrated in the simple FM tutorial patch.
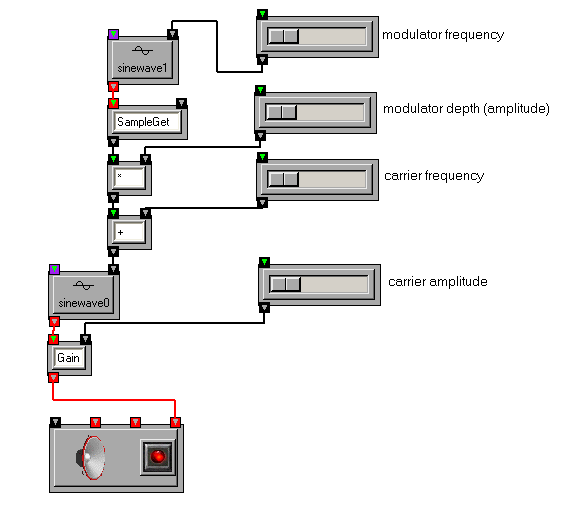
In the FM patch illustrated above, a Sinewave, called a modulator is used to drive the frequency parameter of another Sinewave, called a carrier. (The SampleGet transform is used to extract a single floating-point sample from a block of samples output by the modulator.) FM synthesis will be revisited in more depth later in this chapter.
Additive Synthesis
In the previous section, we used a synthesis function that modeled a simple time-varying sinusoid. We can model arbitrarily complex sounds as a sum of sinusoids:where N is the total number of sinusoids, also called partials. Similar to the single-sinusoid case, each invidiual sinusoid has parameter functions Ai(n), fi(n), and &phii(n) for controling amplitude, frequency and phase, respectively. Each parameter, such as Ai(n) can represent user input, as demonstrated in the additive synthesis tutorial patch. In this patch, the amplitude functions of the partials can be controlled by the user to produce a variety of timbres. The user can also select a fundamental frequency (i.e., pitch) for the synthesized sound. The frequencies of all the partials are locked to integer multiples of the fundamental frequency, creating a set special set of partials called harmonics. Harmonic (or near harmonic) partials are found in many acoustic musical instruments as well as elementary waveforms such as sawtooths, square waves and triangle waves. For example, a band-limited sawtooth waveform of pitch f (not to be confused with the key F) can be approximated as a sum of N sinusoids with frequencies 1f, 2f, 3f,..., Nf (where N < S/2f) and amplitudes 1, 1/2, 1/3,..., 1/N:
You can try to simulate a limited sawtooth waveform in the additive synthesis patch by moving the harmonic-amplitude sliders to 1, 1/2, 1/3, etc. The result should look like this:

Now we will try and approximate a square wave by removing the even partials:
:
The result should sound softer, somewhat "clarinet-like". Compare this result to the output of the Square transform. The Square transform will likely be a bit sharper because its waveform is represented by more than ten partials.
Even with only ten harmonic partials available in this patch, you can synthesize a wide variety of timbres. However, a far richer set of timbres is possible using larger collections of partials and using separate envelope functions for the amplitude, frequency and phase of each sinusoid. The set of envelope functions that describe the amplitude, frequency and phase of a sinusoidal partial are called a sinusoidal track. Thus, this more general additive-synthesis technique is often called sinusoidal-track modeling. To get a better idea of the sinusoidal model representation, it may help to think of 3D space in which the x axis is time, the z axis (depth) is frequency and the y axis (height) is the amplitude. Each track can be represented as a curve traversing this space, as illustrated in the following figure taken from the OpenSoundEdit tool [Chaudhary 1998]:

Variations on sinusoidal models include ``phase vocoder'' models which usually have a fixed number of sinusoids constrained within frequency bands [Dolson 1986], and the more general ``McAulay-Quatieri'' (MQ) sinusoidal models [1978] which are used by most modern computer-based additive synthesizers, including the OpenSoundEdit tool illustrated above, and OSW. In these general models we use, the number of sinusoids can vary between frames, resulting in birth and death events when a sinusoid begins or ends inside a model.
Among the unique features of OSW is its ability to natively express and manipulate sinusoidal models. OSW includes a type Sinusoids, and several transforms for generating, modifying and finally synthesizing sinusoidal models using this data type. If you have opened the additive synthesis tutorial patch, you have already encountered an example of the Sinusoids data type, as well as two important transforms: List2Sinusoids converts OSW lists containing ordered amplitude frequency and phase values into a Sinusoids object, and AddSynth, which synthesizes waveform representations from Sinusoids objects using an additive-synthesis algorithm.
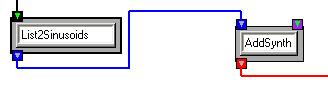
Inlets, outlets and connections of type Sinusoids are distinguished with a bright blue color.
While List2Sinusoids allows you to create sinusoidal models from user input or algorithmically, you can also work with large sinusoidal models stored in the Sound Description Interchange Format (SDIF), which is described in greater detail in chapter 8. You can visit the help patch for AddSynth for an example of synthesis from an SDIF sinusoidal model. On that help page, you will be able to load a large sinusoidal model of a saxophone, and "scrub" back and forth in time and run the model at different rates. This is one of the interesting features of sinusoidal models: controlling the temporal position and rate without affecting the pitch(es) in the model. Compare this to the scrubbing control in the sample looping tutorial, where changing the rate of progress through the sample loop also changes its frequency content, including the pitches.
In addition to its greater temporal mutability, sinusoidal models can be manipulated in ways that are challenging or nearly impossible when working with time-domain waveforms. For example, the DropPartials transform allows you to remove individual sinusoidal components, either by their index within the model, or by a frequency range. DropPartials provides very precise control of the frequencies included and excluded from a sound, precision that would be difficult to accomplish using the filters described in the previous chapter. Another sinusoidal-modeling effect that does not have a simple counterpart in the time domain is Inharmonicity, which allows the relative spacing between partials to expand based on user input or a control function. Inharmonicity gets its name from the fact that it makes harmonic-based models sound less harmonic, because its moves the partials away from integer ratios.
Subtractive Synthesis and Resonance modeling
In additive synthesis, complex sounds are built from simple sinusoidal components. By contrast, in subtractive synthesis, one begins with a frequency-rich sound such as a Phasor, Square, WhiteNoise, a sampled sound, or even a synthesized sinusoidal model and removing portions of the sound via filters.
Subtractive synthesis has a long history dating back to analog synthesizers, which used resonant filters. Subtractive synthesis has also been popular in more recent digital synthesis, which use resonant filters such as those that can be represented using the Biquad and TwoPoleResonz transforms or more complex filter topologies.
Subtractive synthesis with banks of resonant filters can be used to model resonant acoustic systems. This synthesis technique is called resonance modeling. Given an excitation waveform x(n), the resonance of an acoustic system can be modeled as a bank of second-order filters (e.g., similar to Biquad or TwoPoleResonz):
where N is the number of filters in the resonance model, yi(n) is the response of the ith filter, ai is the input scaling coefficient for the filter and b1i and b2i are the feedback coefficients for the previous two samples. The coefficients of each filter can be expressed in terms of more perceptually meaningful parameters: amplitude, frequency and bandwidth:
where S is the sample rate of the output waveform and Ai, fi and ki are the amplitude, frequency and bandwidth, respectively, of the ith resonant filter.
OSW provides a transform, Resonators, that implements a bank of resonant filters as a single unit. It accepts input for the excitation source and an argument of type Resonances that describes the amplitude, frequency and bandwidth of each filter.
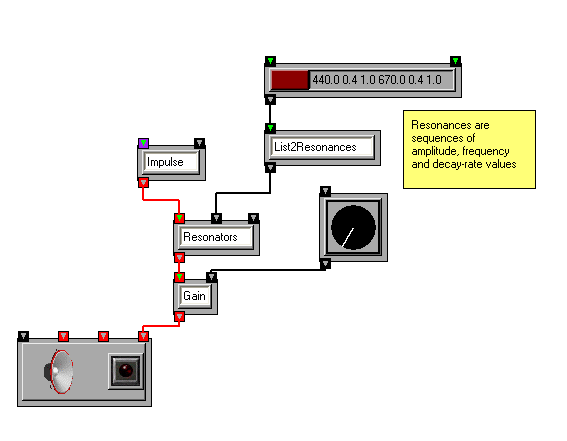
Similar to Sinusoids, the Resonances data type is a very mutable form that can be scaled based on user input or control functions via transforms such as ScaleResonances and JitterRes. Source material for resonance models can be derived from user input or algorithmically via the List2Resonances transform, or from SDIF files via the sdif::ToResonances transform.
If the excitation is an impulse, the resonance can be modeled as a special case of additive synthesis in which the frequency and phase of each sinusoid is constant and the amplitude decays exponentially:
The amplitude Ai determines initial energy of the partial, and the bandwidth ki determines the rate of decay. A smaller bandwidth means a longer decay, and a bandwidth of zero means the resonance stays at constant amplitude. Since the entire evolution of each decaying sinusoid is defined by just three numbers, resonance models require far less data to specify than general additive synthesis. Any instrument that is struck, plucked, or otherwise driven by a single brief burst of energy per tone can be efficiently modeled using impulse-driven resonances. These instruments include pianos, most percussion instruments, plucked strings, and many of the modern extended techniques for traditional orchestral instruments (e.g., key clicks on wind instruments).
Resonances can also be excited by non-impulse signals. Visit the noisy resonance tutorial patch to see an example of a resonance model excited with a noise generator. Mixing various excitation signals, such as breath noise, with resonant systems, such as struck metallic objects, can produce interesting hybrid instrument models.
Although the component resonance partials of a model are excited simultaneously, OSW includes a transform ResPing for exploring a model by exciting individual resonances. This can be used for non-simultaneous effects, such as arpeggiation or "strumming" of resonance models. Visit the Resonance Arpeggiator demo to hear an example of individual resonances excited in sequence.
Wavetables and Waveshaping Synthesis
We have already used several of the oscillator transforms that are available in OSW, such as Sinewave, Phasor, and WhiteNoise. These transforms provide efficient implementations of frequently used oscillator functions. However, there are times when you will want to "create your own oscillators" based on other periodic functions, or require finer control over oscillator functions. The WaveTable transform in OSW allows you to create and control oscillators via a technique called wavetable synthesis. In wavetable synthesis, a small waveform is stored in a table, which in OSW can be either a Table or SampleBuffer, and treated as a single period of a repeating waveform. The WaveTable transform accepts a signal representing phase values an input, and returns the corresponding value from the wave table. Thus, if the phase values repeat with a given frequency, a periodic signal will be generated based on the wavetable with the frequency as its fundamental period.
The most common source of phase input for a wavetable is the Phasor transform (in fact, this is how it gets its name). It can be connected to a WaveTable to sweep through the wavetable periodically.

By default, the WaveTable transform uses a built-in table called /sine as its table. Thus connecting a Phasor to a WaveTable yields another method for generating sine waves. The built in tables available for the WaveTable transform include:
- /sine: one period of a sine function (between 0 and 2p)
- /cosine: one period of a cosine function (between 0 and 2p)
- /exp: the function e-x evaluated between 0 and p
- /sinc: the “sinc” function sin(x)/x evaluated between -p and p. This is a useful function for generating pulse trains via wavetable synthesis.
You can of course load your own tables from external files into a SampleBuffer, or create your own tables on the fly using the Table transform.
So far, we have exclusively used the Phasor transform to provide a regular source of phase information to the wave table. However, any signal can be used as input to a wavetable. When more general signals are used as input to wavetables, the technique is known as wave-shaping synthesis. Load the waveshaping tutorial patch to see what happens when a sine wave instead of a Phasor is used as the source signal for different wavetables.
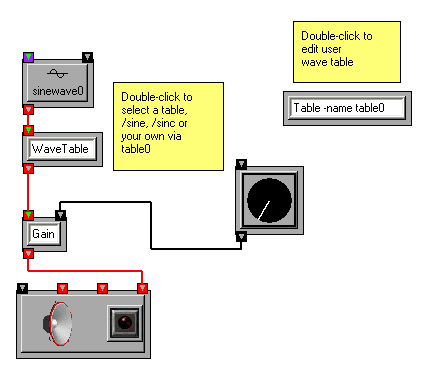
FM Synthesis Revisited
In the context of wavetable synthesis, frequency-modulation can be seen as the application of a modulator to a phasor, as illustrated in the FM tutorial patch. Although this technique is more accurlately called "phase modulation" the name "frequency modulation" is still used in practice and the behavior of this patch is similar to the technique used in "classic FM" synthesizers[Chowning 1985]. The tutorial patch can be extended to include additional modulators (certain popular FM synthesizers with the letter X and various numbers in their names used four or six oscillators arranged in various groups of nested carriers and modulators).
Granular Synthesis
Granular synthesis is an alternative to additive synthesis that is based on a theory developed by Gabor [Roads 1988]. In granular synthesis, a waveform representation is decomposed into tiny waveform representations, called grains. A new waveform is synthesized by selecting a sequence of grains, scaling each grain by an envelope function and combining them in an overlap-add process. If the sequence of grains is exactly the same as the sequence from the analysis, the original waveform representation will be resynthesized. If grains from the analysis sequence are removed without changing the order of the remaining grains, a time-compressed version of the original waveform will be synthesized. If grains are repeated without changing the order (i.e., sequence G1, G2 G3,... becomes G1, G1,..., G2, G2,..., G3,...), then a time-stretched version is synthesized. Thus, similar to additive synthesis, granular synthesis affords independent control over the duration of synthesized waveform representations. If the length of each grain is proportional to the pitch period (i.e., the inverse of the pitch) of the analyzed waveform, then the pitch of original waveform can be independently scaled as well.
OSW includes a transform Granulator that performs real-time granular decomposition and synthesis on waveform representations stored in SampleBuffers. The user can adjust the size of the grains, the number of grains available simulataneously. A typical grain size in granular synthesis is 20ms, or 882 samples at a 44100Hz sampling rate. Experimentation with larger and smaller grain sizes is encouraged.
A final note on synthesis
The survey of synthesis techniques described in this chapter is by no means exhaustive. Many more techniques can be derived from basic building blocks provided by OSW.
Open Sound World User Guide
© 2000-2004 Amar Chaudhary. All rights reserved.